Interactive online versions:
Validation of the Zeeman effect with gepore_zeeman.f (field out of plane)¶
This example demonstrates the use of the gepore_zeeman.f program (a modification of the original gepore.f published in the PNR book chapter [1]) to validate a model with
strong spin-flip scattering
high magnetic field
field out-of-plane (perpendicular to sample surface, but parallel to \(\vec Q\))
magnetization in-plane, therefore perpendicular to field (\(\vec M \perp \vec H\))
The model is a simple slab with a single layer of magnetic material on a non-magnetic substrate.
[1] Majkrzak, C., O’Donovan, K. & Berk, N. (2006). Neutron Scattering from Magnetic Materials, edited by T. Chatterji, pp. 397–471. Amsterdam: Elsevier Science.
[1]:
# Install refl1d if it is not already installed
try:
import refl1d
except ImportError:
%pip install -q "refl1d @ git+https://github.com/reflectometry/refl1d"
import refl1d
[2]:
import numpy as np
from refl1d.validation.gepore_runner import GeporeRunner
start a GeporeRunner instance
[3]:
runner = GeporeRunner()
QS = 0.001 # start value of Q
DQ = 0.0004 # step size in Q
NQ = 80 # number of Q points
Qz = np.arange(NQ) * DQ + QS
Define the sample as a list of layers¶
(note that the in-plane magnetization angle :math:`theta_M` doesn’t matter when the field is out-of-plane)
label |
thickness (A) |
\(\text{SLD}_N\) \((10^{-6}A)\) |
\(\text{SLD}_M\) \((10^{-6}A)\) |
\(\theta_{M}\) \((\text{degrees})\) |
|---|---|---|---|---|
vacuum |
0 |
0.0 |
0.0 |
90.0 |
magnetic |
500 |
8.0 |
2.0 |
90.0 |
substrate |
0 |
2.0 |
0.0 |
90.0 |
[4]:
Aguide = 0.00000001 # nearly zero to avoid division by zero in gepore.f
layers = [
# depth rho rhoM thetaM phiM
[0, 0.0, 0.0, 90.0, 0.0],
[500, 8.0, 2.0, 90.0, 0.0],
[0, 2.0, 0.0, 90.0, 0.0],
]
depth, rhoN, rhoM, thetaM, phiM = list(zip(*layers))
applied field, in Tesla:
[5]:
H = 0.5
Calculating with gepore_zeeman.f¶
The reflectivities are returned from gepore_zeeman.f in the order \((r_g^{++}, r_g^{+-}, r_g^{-+}, r_g^{--})\)
NOTE we use a value of \(\text{EPS} = -\text{Aguide}\)
[6]:
EPS = -Aguide
rgz = runner.run(layers, QS, DQ, NQ, EPS, H, zeeman_corrections=True)
Rgz = [np.abs(r) ** 2 for r in rgz]
Calculating reflectivity using Refl1D¶
magnetic_amplitude returns cross-sections in order \((r_1^{--}, r_1^{-+}, r_1^{+-}, r_1^{++})\), so we need to reverse them here to compare to gepore outputs
[7]:
from refl1d.sample.reflectivity import magnetic_amplitude
r1 = magnetic_amplitude(Qz / 2, depth, rhoN, 0, rhoM, thetaM, 0, Aguide, H)
R1 = np.abs(r1[::-1]) ** 2
Plots¶
[8]:
from matplotlib import pyplot as plt
[9]:
fig = plt.figure()
ax = fig.add_subplot(111)
xs_labels = ["++", "+-", "-+", "--"]
for i, label in enumerate(xs_labels):
ax.plot(Qz, Rgz[i], label=f"gepore {label}")
ax.set_prop_cycle(None)
for i, label in enumerate(xs_labels):
ax.plot(Qz, R1[i], "o", label=f"refl1d {label}", fillstyle="none")
ax.set_ylabel("Reflectivity")
ax.set_xlabel("2*kz_in")
ax.legend()
[9]:
<matplotlib.legend.Legend at 0x7fec46f569c0>
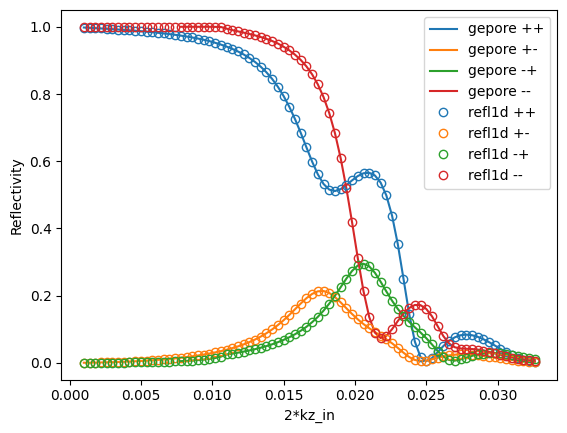
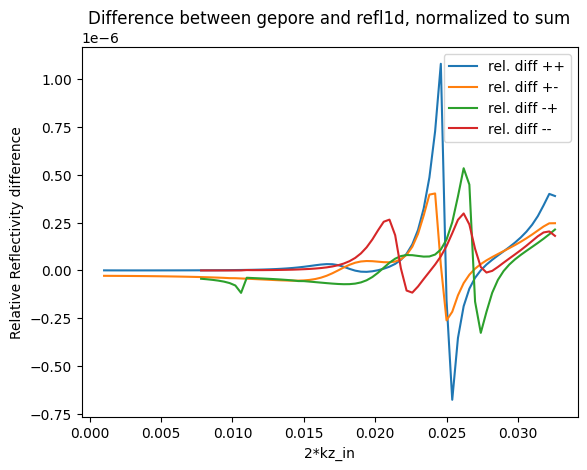
The differences between the two reflectivity outputs are small, and are likely due to differences in the numerical implementation of the reflectivity calculation. Here is a plot of the differences:
[10]:
fig = plt.figure()
ax = fig.add_subplot(111)
for i, label in enumerate(xs_labels):
ax.plot(Qz, 2 * (Rgz[i] - R1[i]) / np.abs(Rgz[i] + R1[i]), label=f"rel. diff {label}")
ax.set_ylabel("Relative Reflectivity difference")
ax.set_xlabel("2*kz_in")
ax.set_title("Difference between gepore and refl1d, normalized to sum")
ax.legend()
[10]:
<matplotlib.legend.Legend at 0x7fec46d23ef0>