Anticorrelated parameters¶
To be sure that the analysis software supports ill-posed problems, we need to present it with problems that we know to be ill-posed. In this example we will look a film with two layers composed of identical materials. The uncertainty analysis should show perfect anticorrelation across the entire parameter range.
(Source code, png, hires.png, pdf)
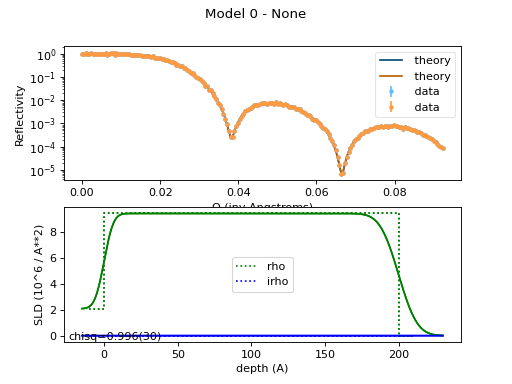
Since silicon and air are defined, the only material we need to define is nickel.
import numpy
from refl1d.names import *
nickel = Material("Ni")
Use a fixed seed so results are reproducible
numpy.random.seed(5)
We need one model with two layers, which together should sum to 200 A. Because of the interface does not extend beyond one layer, we cannot shrink either layer down to zero and preserve chisq, so the parameter values will not dip much below the roughness at the ends of the layer.
sample = silicon(0, 5) | nickel(100, 10) | nickel(100, 10) | air
sample[0].interface.range(0, 20)
sample[1].interface.range(0, 20)
sample[2].interface.range(0, 20)
sample[1].thickness.range(0, 400)
sample[2].thickness.range(0, 400)
Define the probe and simulate data with 5% noise.
T = numpy.linspace(0, 2, 200)
probe = NeutronProbe(T=T, dT=0.01, L=4.75, dL=0.0475)
M = Experiment(sample=sample, probe=probe)
M.simulate_data(noise=5)
We wrap this as a fit problem as usual.
problem = FitProblem(M)
This complete model script is defined in
anticor.py:
import numpy
from refl1d.names import *
nickel = Material("Ni")
numpy.random.seed(5)
sample = silicon(0, 5) | nickel(100, 10) | nickel(100, 10) | air
sample[0].interface.range(0, 20)
sample[1].interface.range(0, 20)
sample[2].interface.range(0, 20)
sample[1].thickness.range(0, 400)
sample[2].thickness.range(0, 400)
T = numpy.linspace(0, 2, 200)
probe = NeutronProbe(T=T, dT=0.01, L=4.75, dL=0.0475)
M = Experiment(sample=sample, probe=probe)
M.simulate_data(noise=5)
problem = FitProblem(M)
We can test how well the fitter can recover the original model by running refl1d with –random:
$ refl1d anticor.py --random --store=T1 --fit=dream --burn=500 --steps=500